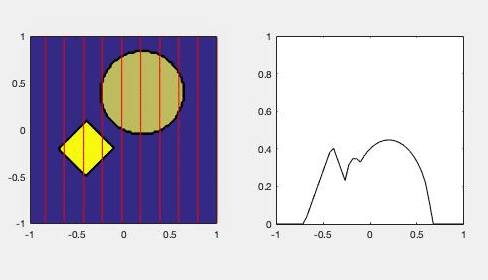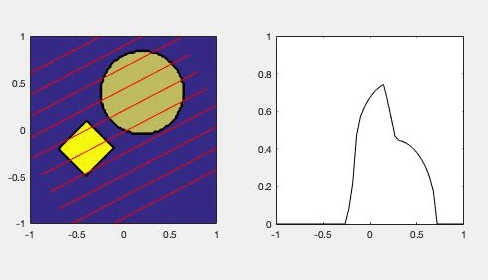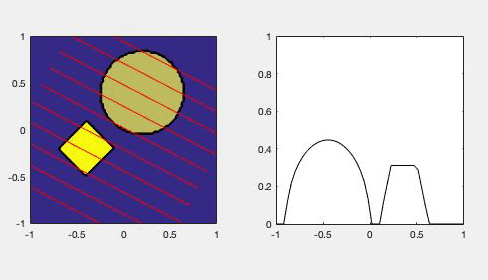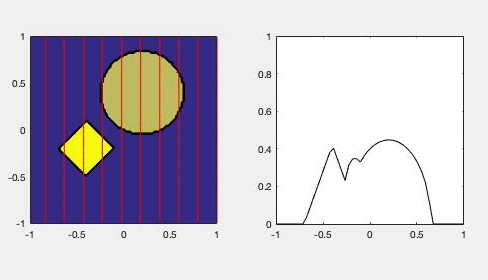
- Education:
- B.S. Mathematics, UT Austin 2009
- M.A. Mathematics, UCLA 2010
- Ph.D. Mathematics, UCLA 2014
- Academic Positions:
- NSF Postdoctoral Fellow, UC Berkeley 2014–2017
- Assistant Professor, Missouri S&T 2017–present
- Photo:


|
Jason Murphy
Assistant Professor Mathematics and Statistics Missouri S&T |
Contact Information:
Office: 313 Rolla Building Phone: (573) 341-4654 Email: jason (dot) murphy (at) mst (dot) edu |
| CV | Research | Teaching |

| Profiles: | arXiv | Google Scholar | MathSciNet |