James R. Friend
210A Mechanical Engineering Annex
University of Missouri-Rolla
Rolla, MO 65401
Daniel S. Stutts
204A Mechanical Engineering Building
University of Missouri-Rolla
Rolla, MO 65401
A zipped PostScript version of this file is here.
Keywords: plates, vibration, piezoelectric motor
The development of piezoelectric motors has spurred an interest in the vibration characteristics of plates laminated with piezoelectric materials. In particular, this paper studies an annular plate composed of one stainless steel lamina and either one or two piezoelectric laminas, a common configuration for piezoelectric motors. The stainless steel layer has teeth milled into the top surface for improved motor behavior. The motion of the teeth is an important characteristic of the motor's performance and is described in detail in this paper. An analytical technique is developed that determines the vibration of the laminate given the input into the piezoelectric layers, and predicts the resulting motion of the teeth.
Hagedorn et al. have demonstrated a simple model for the free vibration of a stator disk [8] and an improved model, using finite element analysis, for the free vibration of a disk with nonuniform thickness [9]. However, forcing due to the piezoelectric elements and the laminated nature of the stator are ignored in their studies. Including these factors into the model makes it more difficult to avoid finite element analysis, and, indeed, Maeno, et al. studied a ring motor including two-body contact mechanics [10] using a finite element analysis program. Bogy and Maeno [11] examined the motor again with contact mechanics and fluid interaction using a combination of analytical and finite element analysis techniques.
Most laminated structures are modeled as a collection of layers with specific material properties. Several approaches to modeling the laminate are possible; classical lamination theory [12], first-order and higher-order shear deformation theories with or without rotary inertia [13,14], and a relatively unique and complex procedure by Reddy, et al. [15,16] are representative of common solution techniques. Tzou has developed general laminated composite deep-shell equations [17-20] specifically for piezoelectrically forced structures. However, all of these methods are limited in their capability to model asymmetric laminated structures with closed-form solutions. With the exception of classical lamination theory and a few cases with the first-order shear deformation theory, the problem to be solved always requires finite element analysis. While finite element analysis (FEA) is indispensable for many applications, particularly with complex geometries, it is inconvenient for system design. Each design iteration requires a new finite element mesh to be generated and a new numerical solution to be obtained. This process, known as FEA parametric optimization, is computationally expensive, and it provides a compelling reason to seek analytical solutions.
Approaching the problem with the caveat that all solutions must be closed-form solutions has its own difficulties, however. There is no assurance that the solution will resemble the "correct answer" after making necessary approximations and there may be no solution at all for many complex systems. Finite element analysis is avoided by using judicious approximations that retain the behavior of the laminated structure and the teeth. The class of piezoelectric motors modeled are based on the thin annular plate as shown in Figure 1. The analysis presented here is applicable to stator geometries from a solid circular plate (b=0) to an annular ring (b/a >= 0.9) where shear deformation and rotary inertia are negligible. The modeling approach described here represents an enhancement of the current modeling literature by (1) predicting steady-state stator motion directly from prescribed electric fields induced in the piezoelectric laminas, (2) accounting for the asymmetric laminated structure in an approximate sense, and (3) modelling the kinematics of thestator teeth. The ability to predict the motion of the stator teeth is essential for subsequent modelling of the interaction between the stator and rotor which is required to predict motor performance.
Figure 1. Thin annular plate geometry
.
The double dot indicates an inner product over two indices of the tensors (A list of symbols is provided in the nomenclature at the end of this paper). This relatively general form is difficult to work with, but by making two assumptions, the equations may be simplified. For the entire volume of an elastic body, excluding the exterior surfaces and interior flaws, the stress tensor is symmetric, so an initial assumpution is that the stress tensor is symmetric throughout the area of interest. Further, for this application (and for most others), the electrical field travels through the material at much higher speeds than the strain field -- fast enough to assume that from the perspective of the mechanical motion of the plate, the electrical fields in the piezoelectric laminas change instantaneously. In other words, the motion of the piezoelectric laminates is quasistatic. By contracting the tensor notation as in Auld [21] and applying the symmetric stress tensor assumptions, equation simplifies to
.
The stress due to the electric field in the piezoelectric laminas is
.
The stress-strain relationship in equation will be taken into account in the equation for the transverse motion of the plate below.
The stress in the piezoelectric plate flexes the overall structure. This flexure can occur through transverse deflection of the entire structure or by bending about the midplane of the plate as shown in Figure 2.
Figure 2. Deflection of piezoelectric laminated structures
Since the piezoelectric elements are situated away from the midplane and are thin in comparision to the thickness of the stainless steel layer, the in-plane expansion and contraction of the laminate is much less than the bending of the laminate. In the following sections, a dynamical model of the vibration of the stator and teeth located on it due to excitation of the piezoelectric plates by harmonically varying electric fields will be developed.
Figure 3. Stator plate with teeth - (1,4) mode
The equation of transverse motion [22] of the plate neglecting shear deformation and rotary inertia is
,
where f(r,[[theta]],t) denotes general forcing,
is the biharmonic operator in polar coordinates [23], and the reduced bending
stiffness,
,
of the composite plate [12] is the (1,1) component of the matrix D given
by
.
The components of A, B, and D, respectively, are
,
,
and
.
Equation is an approximation for the composite nature of the stator ignored in the current literature. The full equations for the general composite plate including asymmetry are extremely complex and are regarded as being intractable in closed form. The lamination structure of the stator is indicated in Figure 4 for motors with two piezoelectric layers; motors with only one piezoelectric layer are similar.
Figure 4. Lamination structure and nomenclature
For the unforced case (f(r,[[theta]],t) = 0), a separable, temporally harmonic solution may be assumed;
.
Equation becomes
.
By dividing through by
and substituting [[lambda]]4 for [[rho]]h[[omega]]2/
,
equation becomes
or
.
This equation will allow solutions of the same form as the following equation:
.
Separating the spatial variables,
,
equation becomes
by grouping the r-dependent terms on the left and the [[theta]]-dependent terms on the right. In the usual manner, the two leftmost parts of equation (13) must be equal to a constant since they are equal to each other for all r>0 and [[theta]]. That constant is called n2. This allows the separation of equation into the two following equations:
and
.
The solutions for the two equations are
and
for the m-th radial and n-th circumferential modes and where
[[phi]] is an arbitrary phase angle which is typically chosen to be
zero. The terms Jn and In are Bessel's first and second
functions of order n; Yn and Kn are Bessel's modified
first and second functions of order n. All of the constants
and B are linearly dependent to within a single constant if the boundary
conditions are specified; i.e., they may all be found in terms of a
single constant if the information about the loading and deflection on the
boundary is given. The complete solution for the plate is
.
The constant B has been absorbed into the
and so the hi-hats are dropped.
For the piezoelectric motor, the plate is annular and is not loaded on either the inner or outer radius with loads as shown in Figure 5.
Figure 5. Piezoelectric motor plate (with two piezoelectric layers)
The boundary conditions for this configuration with Kirchoff's approximation are
and
for both the inner and outer radii of the annular plate as suggested by Raju. Mr is the resultant (mechanical) moment on the inner and outer radial faces of the plate and Vr is the resultant shear at the same locations. Since the moment and shear (normal to the plate) are both zero on the inner and outer boundaries, equations and are set equal to zero. The solution for the plate, equation , must be substituted into equations and to give four equations in terms of the parameter [[lambda]]n and the four constants Ai; i.e.
,
where C1j refers to the substitution of equation into the moment equation for the inner radius and collected in terms of Ai. Similarly, C2j refers to the substitution of equation into equation for the outer radius, C3j refers to the substitution of equation into equation for the inner radius, and C4j refers to the substitution of equation into equation for the outer radius. Since all of the Ai are not zero for a useful solution, this problem becomes an eigenvalue problem for [[lambda]]mn, which is embedded in the Cij. Taking the determinant of the matrix [Cij] and solving for [[lambda]]mn will give the resonant frequency of the plate for the (m,n) mode by solving for the resonant frequency [[omega]]mn in
.
Finding the mode shape for a given (m,n) requires the use of equation again. Assuming that A4 is unity, the remaining Ai may be found in terms of A4, which would determine all of the Ai within a constant. Setting A4 = 1 in equation and simplifying gives
,
an overdetermined equation. Using only the first three rows of the matrix, the remaining Ai may be found;
.
.
Structural damping may be included (as equivalent viscous damping) in the plate as a part of the general forcing term. Including simple transverse forcing T3 (illustrated in Figure 6) and damping, the forcing term becomes
where cv is the equivalent viscous damping constant. Substitution of the forcing term and equation (25) into (4) gives
Transverse piezoelectric forcing may be be written as
,
assuming transversely induced electrical fields. From the analysis on the free plate,
,
so equation becomes
.
Figure 6. Transverse forcing
Assuming the forcing due to the piezoelectric plates is invariant with respect to the radial coordinate, reasonable for most motors of this geometry, the m subscript and summation over m may be dropped. Multiplying both sides by U3k, where k is necessarily equal to n gives
.
In practice, the induced forcing is usually designed to excite a single mode by ensuring that the forcing closely matches the desired mode, so the complete summation of modes over both n and k collapses into a single summation over n with a given constant k. Integrating both sides over the plate midplane to exploit the orthogonality of the modes gives
,
or
.
The integrals may move within the infinite sum by assuming that the plate surface is continuous with derivatives that are continuous to the second order (class C2). Since each mode of plate vibration is orthogonal to every other mode,
Hence, all the terms in the infinite sum in equation vanish except for the one when n = k. A single ordinary differential equation remains to be solved for the modal participation factor of mode k;
,
where
,
,
and
.
The steady-state harmonic forcing is
.
The steady-state harmonic response of the plate vibration is the most important part of the motor's operation, since the transient part lasts only a few milliseconds for most motors. Since the response will be harmonic, the solution for equation is
.
Substituting this into equation and solving for [[Lambda]]k gives
where
.
The magnitude of the response is
,
and the phase lag angle [[phi]]k is
.
If there is only one mode being excited in the plate, then only one solution of the modal participation factor is necessary, making the solution process relatively simple.
This derivation does not include the forcing by the piezoelectric layers through moments about the midplane, however. Moment forcing may be included as a set of additional terms in equation which manifest themselves on the right side of equation as supplementary forcing. These terms may be derived by expressing the energy put into the plate by moment forcing.
From Soedel [24], the energy input into the plate from moment forcing is
where
and
Figure 7 illustrates the orientation of the forcing.
Figure 7. Moment forcing on plate
Taking the variation of equation ,
,
where
and
.
So equation becomes, after integration by parts,
.
The double integral is the only portion relevant to the forcing; after substitution and modal expansion, it simplifies to
.
The modal loading of the plate, Fk*, expressed by equation becomes
.
Fk* expresses the modal loading on the plate for any fixed point in time on the k-th mode. It only depends on the spatial variables r and [[theta]]. In a piezoelectric motor, the induced fields in the piezoelectric plate and thus the loading by a single piezoelectric laminate could be assumed to be radially constant and azimuthally harmonic as shown in Figure 8;
,
where
is the peak field strength induced in the piezoelectric lamina. If a second
piezoelectric lamina is present, the induced in it may be out of phase with the
field induced in the other piezoelectric layer;
,
where [[phi]]PZT is the phase angle between the two piezoelectric laminas. This angle between the two layers is necessary to create a traveling wave in many piezoelectric motors. Notice that both layers are assumed to have the same peak electrical fields and the same thickness.
Figure 8. Sinusoidal electric field distribution
The moment forcing on the plate due to planar expansion of the piezoelectric plate can be expressed by
.
illustrated by Figure 9. The analogous expression for the radial moment is
These equations give the moments exerted by a single piezoelectric layer next to the stainless steel layer excited with a temporally harmonic electric field distribution. For two piezoelectric layers, the radial and circumferential moments are
and
,
illustrated by Figure 10. By assuming the electric field is constant in the radial direction, equation can be simplified slightly since the derivative of the moment Mr with respect to the radial direction is zero;
.
Figure 9. Moment forcing by one piezoelectric plate on motor about radial axis
Figure
10. Moment forcing by two piezoelectric plates on motor about radial axis
for a plate vibrating in the n-th mode. Define a vector from the center of the annular plate at its midplane to a point in the midplane of the deformed plate as
.
To determine the motion of a tooth on the surface of the plate, a unit vector normal to the surface is needed. Taking the derivative of equation with respect to r (holding time fixed),
,
and taking the derivative of equation with respect to [[theta]] and dividing by r gives
,
two equations which represent tangent vectors along the surface at (r,[[theta]]) in the radial and circumferential directions, respectively. Taking the cross product of these two vectors and normalizing to find the unit normal vector to the surface,
,
gives
.
Then the vector to the end of the tooth has the following form:
for a motor with a single piezoelectric layer or
for a motor with two layers of piezoelectric material. Fully expanded, equation is
.
This gives the location of the center of the top of each tooth if we know its location on the plate as shown in Figure 11. Effectively equation transforms the plate vibration solution into a tooth displacement solution for any point (r,[[theta]]). The velocity of the teeth as they move can be found by taking the derivative of equation with respect to time;
,
which, after some expansion and algebra (
for this structure), is,
.
After assuming products of derivatives are negligible, equation simplifies to
.
For the piezoelectric motor, the location of the teeth is specified as a part of the design. To make it easier to determine the motion of the teeth, the location of each tooth is based on an index i, its arc-width (r[[theta]])T, the arc-width of the gap between each tooth (r[[theta]])gap, the location of the inner radius of the teeth rTin, and the location of the outer radius of the teeth rTout. The location of the center of each tooth is, then,
,
where i is the tooth selected. These two equations can be used in equation to describe the motion of those teeth.
Figure 11. Schematic of tooth kinematics
Work is currently underway to extend this model to account for the contact mechanics between the rotor and stator, and these results will be presented in a subsequent paper. This extension will allow the prediction of motor performance metrics such as torque and speed. Model predictions can then be compared to experimentally measured performance metrics in a variety of commercially available piezoelectric motors.
2. A. KUMADA Piezoelectric Revolving Resonator and Ultrasonic Motor. US Patent No. 4,868,446, September 19, 1989. 10 Claims, 17 Drawing Sheets.
3. A. KUMADA Ultrasonic Motor Using Bending, Longitudinal, and Torsional Vibrations. US Patent No. 4,642,509, February 10, 1987. 10 Claims, 14 Drawing Sheets.
4. A. KUMADA, T. IOCHI, and M. OKADA Piezoelectric Revolving Resonator and Single-Phase Ultrasonic Motor. US Patent No. 5,008,581, April 16, 1991. 6 Claims, 6 Drawing Sheets.
5. T. SASHIDA and T. KENJO 1993 An Introduction to Ultrasonic Motors. Monographs in Electrical and Electronic Engineering, Vol. 28, eds. P. Hammond, T. J. E. Miller, and S. Yamamura. Oxford: Clarendon Press, 242.
6. T. SASHIDA, Motor Device Utilizing Ultrasonic Oscillation. US Patent No. 4,562,374, December 31, 1985. 29 Claims, 22 Drawing Sheets.
7. S. UEHA AND Y. TOMIKAWA 1993 Ultrasonic Motors -- Theory and Applications. Monographs in Electrical and Electronic Engineering, Vol. 29, eds. P. Hammond, T. J. E. Miller, and S. Yamamura. Oxford: Clarendon Press, 297.
8. P. HAGEDORN and J. WALLASHEK 1992 Journal of Sound and Vibration 155, 31-46. Travelling Wave Ultrasonic Motors, Part I: Working Principle and Mathematical Modeling of the Stator.
9. P. HAGEDORN, J. WALLASHEK, and W. KONRAD 1993 Journal of Sound and Vibration 168, 115-122. Travelling Wave Ultrasonic Motors, Part II: A Numerical Method for the Flexural Vibrations of the Stator.
10. T. MAENO, T. TSUKIMOTO, and A. MIYAKE 1990 7th IEEE International Symposium on Application of Ferroelectrics, In Kangawa, Japan, 535-538. The Contact Mechanism of an Ultrasonic Motor.
11. T. MAENO, and D. BOGY 1992 IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 39, 675-682. Effect of the Hydrodynamic Bearing on Rotor/Stator Contact in a Ring-Type Ultrasonic Motor.
12. J. E. ASHTON, and J. M. WHITNEY 1970 Theory of Laminated Plates, Vol. IV. Progress in Materials Science Series, Stamford, CN: Technomic, 153.
13. R. D. MINDLIN 1951 Journal of Applied Mechanics, Transactions of the ASME, Series E 73, 31-38. Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic, Elastic Plates.
14. J. N. REDDY 1990 Shock and Vibration Digest 22, 3-17. A Review of Refined Theories of Laminated Composite Plates.
15. J. N. REDDY 1990 Journal of Nonlinear Mechanics 25, 677-686. A General Third-Order Nonlinear Theory of Plates with Moderate Thickness.
16. A. NOSIER, R. K. KAPANIA, and J. N. REDDY 1993 AIAA Journal 8, 2335-2346. Free Vibration Analysis of Laminated Plates Using a Layerwise Theory.
17. H. S. TZOU 1990 Proceedings of the 1990 ASME International Computers in Engineering Conference and Exposition in Boston, Maryland, 473-480. Electromechanical Dynamics of Piezoelectric/Elastic Structures Applied to Micro-Actuation and Distributed Structural Identification/Controls.
18. H. S. TZOU 1991 Journal of Dynamic Systems, Measurement and Control 113, 500-505. Distributed Modal Identification and Vibration Control of Continua: Piezoelectric Finite Element Formulation and Analysis.
19. H. S. TZOU 1993 Piezoelectric Shells : Distributed Sensing and Control of Continua. Solid Mechanics and Its Applications, Vol. 19. Boston: Kluwer Academic, 468.
20. H. S. TZOU, and J. ZHONG 1992 Journal of Dynamic Systems, Measurement and Control 115, 506-517. Electromechanics and Vibrations of Piezoelectric Shell Distributed Systems.
21. B. A. AULD 1990 Acoustic Fields and Waves in Solids (two volumes). Malabar, FL: Krieger, second edition.
22. P. RAJU 1962 Journal of the Aeronautical Society of India 14, 37-50. Vibrations of Annular Plates.
23. B. D. AGARWAL and L. J. BROUTMAN 1990 Analysis and Performance of Fiber Composites. SPE Monographs, New York: John Wiley and Sons, second edition, 449.
24. W. SOEDEL 1990 Vibrations of Shells and Plates. Mechanical Engineering, Vol. 10, eds. L. Faulkner and S. Menkes. New York: Marcel Dekker, 366.
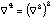 Biharmonic operator (see equation )
Ai,
Biharmonic operator (see equation )
Ai,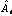 ,B Constants (i = 1,2,3,4)
A Composite plate in-plane stiffness matrix
B Composite coupling matrix
[[beta]][[theta] Rotation angle of plate about the azimuthal axis
]
[[beta]]r Rotation angle of plate about the radial axis
c, cIJ Material stiffness tensor (cE is measured with a constant
electric field)
d() First variation of ()
D, Dij Composite plate bending stiffness
D*,
,B Constants (i = 1,2,3,4)
A Composite plate in-plane stiffness matrix
B Composite coupling matrix
[[beta]][[theta] Rotation angle of plate about the azimuthal axis
]
[[beta]]r Rotation angle of plate about the radial axis
c, cIJ Material stiffness tensor (cE is measured with a constant
electric field)
d() First variation of ()
D, Dij Composite plate bending stiffness
D*, 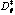 Reduced composite plate bending stiffness (see Ashton, et
al. [12])
Reduced composite plate bending stiffness (see Ashton, et
al. [12])
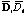 Charge displacement vector
E* Peak-to-peak electric field induced in piezoelectric plate
e, eIj Piezoelectric stress tensor
[[epsilon]], Permittivity tensor ([[epsilon]]T is measured with a
[[epsilon]]ij constant stress field, [[epsilon]]S is measured with a
constant strain field)
E, Ej Induced electric field tensor
E3 Electric field induced transversely across piezoelectric
plate
Em Energy introduced into plate from moment forcing
er, e[[theta]], Unit vectors along coordinate axes
ez
[[phi]] Phase angle of induced electric field (azimuthal)
F([[theta]]) Azimuthal solution of transverse plate motion
[[phi]]k Phase angle for the k-th modal solution of freely vibrating
plate
Fk Modal forcing
[[phi]]PZT Rotation angle between the bottom piezoelectric layer and
the top piezoelectric layer
[[phi]]t Phase angle of induced electric field (temporal)
[[eta]] Modal participation factor (0 <= [[eta]] <= 1)
h Thickness of the plate
hi Thickness of lamina i (i = PLATE, PZT)
i, I, j, J Spatial subscripts ( = 1,2,3)
j Imaginary unit
Charge displacement vector
E* Peak-to-peak electric field induced in piezoelectric plate
e, eIj Piezoelectric stress tensor
[[epsilon]], Permittivity tensor ([[epsilon]]T is measured with a
[[epsilon]]ij constant stress field, [[epsilon]]S is measured with a
constant strain field)
E, Ej Induced electric field tensor
E3 Electric field induced transversely across piezoelectric
plate
Em Energy introduced into plate from moment forcing
er, e[[theta]], Unit vectors along coordinate axes
ez
[[phi]] Phase angle of induced electric field (azimuthal)
F([[theta]]) Azimuthal solution of transverse plate motion
[[phi]]k Phase angle for the k-th modal solution of freely vibrating
plate
Fk Modal forcing
[[phi]]PZT Rotation angle between the bottom piezoelectric layer and
the top piezoelectric layer
[[phi]]t Phase angle of induced electric field (temporal)
[[eta]] Modal participation factor (0 <= [[eta]] <= 1)
h Thickness of the plate
hi Thickness of lamina i (i = PLATE, PZT)
i, I, j, J Spatial subscripts ( = 1,2,3)
j Imaginary unit 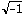 Jn, In Bessel's original and modified functions of the first kind,
respectively
[[lambda]] Eigenvalue of characteristic equation of plate
m Radial mode number (number of circular modal lines)
M[[theta]] Moment forcing about the azimuthal direction
Mr Moment forcing about the radial direction
n Mode shape number or number of diametral modal lines
[[nu]] Poisson's ratio
N, eN Vector and unit vector normal to the deformed plate's
midplane, respectively
Nk Modal normalization factor
Q11 Reduced stiffness (= Q22 =
Jn, In Bessel's original and modified functions of the first kind,
respectively
[[lambda]] Eigenvalue of characteristic equation of plate
m Radial mode number (number of circular modal lines)
M[[theta]] Moment forcing about the azimuthal direction
Mr Moment forcing about the radial direction
n Mode shape number or number of diametral modal lines
[[nu]] Poisson's ratio
N, eN Vector and unit vector normal to the deformed plate's
midplane, respectively
Nk Modal normalization factor
Q11 Reduced stiffness (= Q22 = 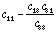 for all layers since PZT is
axisymmetric about the direction of poling after poling)
See [17]
[[rho]] Density of the plate
r Radial variable
R(r) Radial solution of transverse plate motion
rTin, rTout Radius of inner and outer edges of the teeth, respectively
(r[[theta]])T, Arclength of tooth and gap
(r[[theta]])gap
S, SJ Strain tensor
t Time
for all layers since PZT is
axisymmetric about the direction of poling after poling)
See [17]
[[rho]] Density of the plate
r Radial variable
R(r) Radial solution of transverse plate motion
rTin, rTout Radius of inner and outer edges of the teeth, respectively
(r[[theta]])T, Arclength of tooth and gap
(r[[theta]])gap
S, SJ Strain tensor
t Time
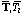 ,TI Stress tensor, components, and stress components due to
electrical excitation, respectively
Ti Forcing in the i-th direction
Tr, T[[theta]] Vectors tangent to midplane surface in radial and azimuthal
directions, respectively
[[theta]] Azimuthal variable
u3 Transverse displacement (time domain)
U3 Transverse displacement (frequency domain)
[[omega]] Circular frequency (rad/s)
[[omega]] Circular frequency of applied forcing
[[omega]]k Resonant circular frequency of k-th mode of plate
x Vector to a point on the midplane of the annular plate from
the center at the midplane
xT Vector to the end of a tooth from the center of the midplane
Yn, Kn Bessel's original and modified functions of the second
kind, respectively
zk Distance from the midplane of the composite plate to the
k-th interface (k = 0 indicates the top of the plate, k = 1
indicates the interface between the stator and the top PZT
plate, and so on)
[[zeta]]k Damping of k-th mode of plate
,TI Stress tensor, components, and stress components due to
electrical excitation, respectively
Ti Forcing in the i-th direction
Tr, T[[theta]] Vectors tangent to midplane surface in radial and azimuthal
directions, respectively
[[theta]] Azimuthal variable
u3 Transverse displacement (time domain)
U3 Transverse displacement (frequency domain)
[[omega]] Circular frequency (rad/s)
[[omega]] Circular frequency of applied forcing
[[omega]]k Resonant circular frequency of k-th mode of plate
x Vector to a point on the midplane of the annular plate from
the center at the midplane
xT Vector to the end of a tooth from the center of the midplane
Yn, Kn Bessel's original and modified functions of the second
kind, respectively
zk Distance from the midplane of the composite plate to the
k-th interface (k = 0 indicates the top of the plate, k = 1
indicates the interface between the stator and the top PZT
plate, and so on)
[[zeta]]k Damping of k-th mode of plate