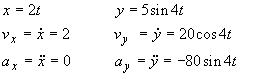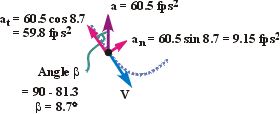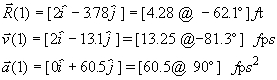Example 2-3: Use of Parametric Equations

A particle moves along a path described by the vector equation

with  R  given in meters and time in seconds.
     (a)  Determine the path equation; 
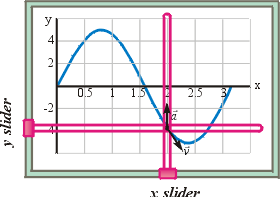
     (b)  Plot the path; 
Also determine 
     (c) The velocity and acceleration vector equations; 
     (d) The position, velocity, and acceleration vectors at time t =  sec; 
     (e)  The angle between the acceleration vector and the velocity vector; 
      (f)  The normal and tangential components of acceleration.

(a) Eliminate time t from the  parametric equations

and             

to obtain the path equation:         

(b)  Plot the path.  Note that though the path shows both an upper and lower leg, the particle only moves along the upper leg.

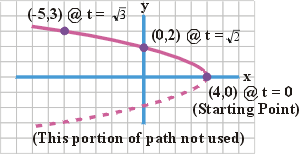
(c) Velocity and acceleration vector equations are found from time derivatives of the vector position equation.

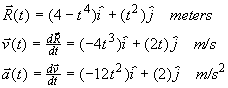
(d)  At time t =  sec, the position, velocity and acceleration vectors are, in both cartesian and polar form:

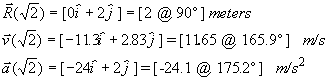
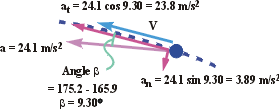
(e)  The angle, b, between the  v  and a  vectors, as shown above, is 9.30°.

(f)  The normal and tangential components of acceleration (shown above) are easily found once b is known.

Note:  The angle b between  v  and a  can also be found from the dot product:

 
Thus,

An x-y plotter consists of an x slider and a y slider, with a pen located at the intersection of the two sliders.  Both sliders are capable of moving independently in time in order to plot virtually any kind of curve.  If for a particular plot the pen position is described by x = 2t and y = 5 sin 4t , where x and y are in feet and t is in seconds, do the following: 
     (a)  Determine the path equation; 
     (b)  Plot the path; 
Also determine 
     (c)  The velocity, and acceleration vectors at x = 2 ft; 
     (d)  The angle between the acceleration vector and the velocity vector; 
     (e)  The normal and tangential components of acceleration.

(a) Eliminate time t from the  parametric equations

and             

to obtain the path equation: 

(c) Velocity and acceleration components are found from time derivatives of the parametric equations:

At x = 2 ft, time is t = 1 sec (since x = 2t ). The position, velocity and acceleration vectors are, in both cartesian and polar form:

(d)  The angle, b, between the v  and a  vectors, as shown above, is 8.70°.

(e)  The normal and tangential components of acceleration are easily found once b is known.  These are shown in the picture above.