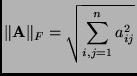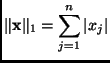
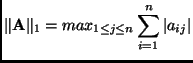
For most of our applications, we will use one of three possible vector norms as already identified. The question that faces us is what are the compatible operator norms induced by these vector norms.We will answer the question once in detail and leave the other two for discussion later.
Let's begin with the 1-norm.
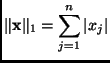
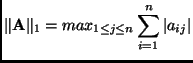
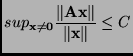
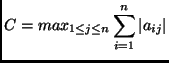
To this end, let ![]() be defined as above. For
be defined as above. For
![]() , we have
, we have
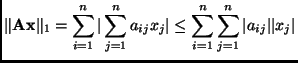
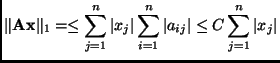
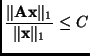
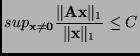
Now that we have this bound, what remains to be shown is that the is a vector
![]() such that
such that
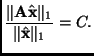
To find such a vector
![]() , we note that there is a number
, we note that there is a number ![]() such that
such that
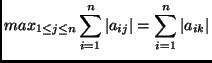
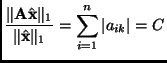
So the operator norm induced by the 1-norm is the maximum value of the sum of the absolute value of the entries in a column.
Let use examine the other induced operator norms.

On the basis of these examples, you might guess that the operator norm induced by the standard Euclidean norm is