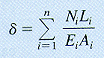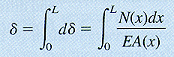Change in Length of Axially Loaded Members

springs

natural length,  L - unstressed, relaxed, or free length

stiffness, k - spring constant; the force required to produce a unit elongation

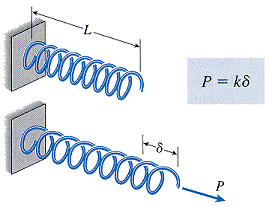
spring testing

 

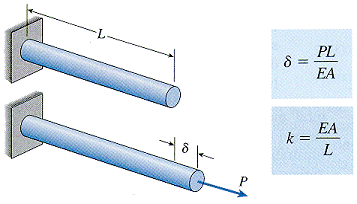
prismatic bars

prismatic bar - structural member having a straight longitudinal axis and constant cross section throughout its length

elongation, δ (+ stretching, - shortening)

Assumptions

• load acts through centroid of cross section
• homogeneous material
• linear-elastic material (i.e., follows Hooke's law)

 

bars with prismatic segments The bar may consist of several prismatic segments, each with different: axial forces dimensions materials Solution technique Identify segments (i=1,2,...,n) Determine internal forces in each segment Determine change in length of each segment Sum (+ tension, - shortening)
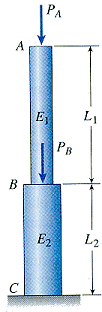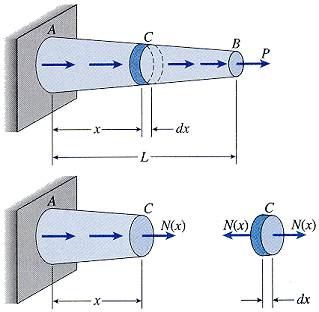tapered bars The bar may have: varying cross-sectional area varying axial force (e.g. centrifugal forces, friction forces, weight of bar in a vertical position) Solution technique cut differential element of length dx balance forces to determine N(x) determine A(x) integrate over the length of the bar