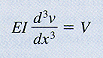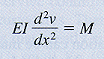Differential Equations of the Deflection Curve

The St. Louis Arch sways about
 one inch in a 20 mph wind.  It is
designed to sway up to 18 inches
in 150 mile per hour winds. (source)

With a wind of 110 miles per hour, the 1454-ft
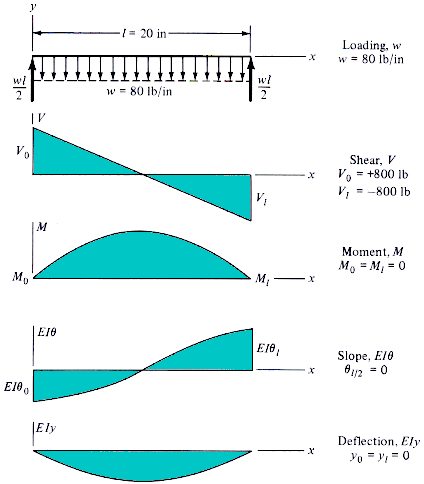
Empire State Building gives 1.48 inches. (source)

 

example

from Mechanical Engineering Design, 5th Ed., by J.E. Shigley and C.R. Michke, McGraw-Hill, 1989, p95

 

terms

plane of bending - deflections will occur in a plane if the beam is symmetric around this plane

deflection, ν - the displacement of any point along the beam from its original position, measured in the y direction

deflection curve

coordinate axes

angle of rotation, θ - the angle between the x-axis and the tangent to the deflection curve

slope of the deflection curve: dν/dx = tan θ

tan θ = θ for small angles
 

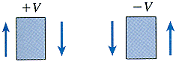
sign conventions

  1. the x and y axes are positive to the right and upward
  2. the deflection ν is positive upward
  3. the slope dν/dx and angle of rotation θ are positive when counterclockwise with respect to the positive x axis
  4. the curvature κ is positive when the beam is bent concave upward
  5. the bending moment M is positive when it produces compression in the upper part of the beam

 

Differential Equations

load equation
shear-force equation
bending-moment equation

 

solution technique

 

assumptions