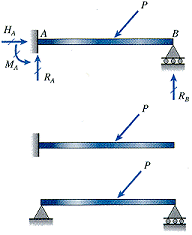
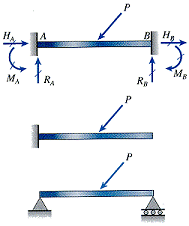
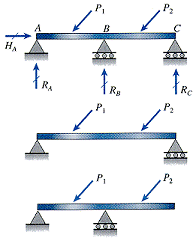
| Propped cantilever beam | Fixed-end beam | Continuous beam | ||
 |
 |
 |
Introduction
statically determinate beamsthe number of reactions equals the number of independent equilibrium equations
- determine reactions
- determine shear forces and bending moments
- determine stresses and deflections
statically indeterminate beams
the number of reactions exceeds the number of independent equilibrium equations
Most of the structures we encounter in everyday life (automobile frames, buildings, aircraft) are statically indeterminate. However, they are much more complex than beams and must be designed by sophisticated analytical techniques. Many of these techniques rely on the concepts presented in this chapter.
degree of static indeterminacy
the number of reactions in excess of the number of equilibrium equations
static redundants
the excess reactions
released structure or primary structure
the structure that remains when the redundants are released
- must be stable -- can carry loads
- must be statically determinate -- all force quantities can be determined from equilibrium alone
Types of Statically Indeterminate Beams
Propped cantilever beam Fixed-end beam Continuous beam
Analysis by the Differential Equations of the Deflection Curve
This technique involves symbolically solving the differential equations of the deflection curve, just as for a statically determinate beam. However, unknown quantities will now include integration constants and redundant reactions. Various conditions must be applied to solve for all of the unknowns.
This technique is only useful for simple beam and loading situations.