Combined Loadings

introduction


aircraft, building, oil platform, mine, bio

The objective is to determine the largest stresses anywhere in the structure.  No new theories are involved -- only applications of previously derived formulas and concepts.

axial σ = N/A
torsion τ = Tc/J
flexure s = -My/I
shear τ = VQ/Ib
pressure σ = pr/t
σ = pr/2t
combined σ = Σσi
 τ = Στi

 

superposition

We will superimpose the stresses and strains caused by each load acting separately and then add those in the same direction,

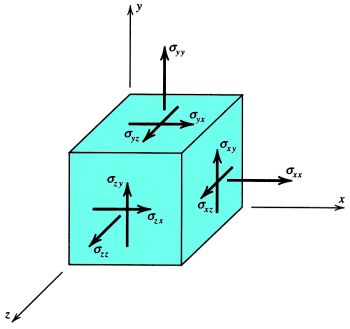
σx = Nx/Ax + Fb/Ab + pr/t + pr/2t -p - Myy/Iy - Mzz/Iz
σy = Ny/Ay + Fb/Ab + pr/t + pr/2t -p - Mxx/Ix - Mzz/Iz
σz = Nz/Az + Fb/Ab + pr/t + pr/2t -p - Mxx/Ix - Myy/Iy

τxy = V/A + Txcx/Jx + Tycy/Jy + VxQx/Ixbx+ VyQy/Iyby
τyz = V/A + Tycy/Jy + Tzcz/Jz + VyQy/Iyby+ VzQz/Izbz
τzx = V/A + Txcx/Jx + Tzcz/Jz + VxQx/Ixbx + VzQz/Izbz

eliminating terms as needed.

see M15.1 to M15.7

 

method of analysis

  1. Select a point in the structure where the stresses and strains are to be determined. (usually where the stresses are the largest)
  2. For each load, determine the stress resultants at the point. (look at axial force, twisting moment, bending moment, shear force, pressure)
  3. Calculate the normal and shear stresses due to each stress resultant. (σ = P/A, τ = Tc/J, σ =My/I, τ = VQ/Ib, σ = pr/t)
  4. Combine the individual stresses. (obtain σx, σy, τxy at the point)
  5. Determine the principal stresses and maximum shear stresses.
  6. Determine the strains using Hooke's law.
  7. Repeat the process for additional points, until you are confident you have found the largest stresses anywhere in the structure