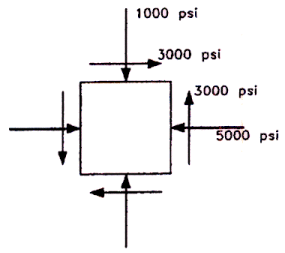
18. For stress conditions on the element shown, find the principal stresses and the plane on which the maximum principal stress acts.

tan(2q_p) = 2t_xy / (s_x-s_y)

s_u = (s_x+s_y)/2 + (s_x-s_y)/2 cos(2q) + t_xysin(2q)
s_v = (s_x+s_y)/2 - (s_x-s_y)/2 cos(2q) - t_xysin(2q)
t_uv = -(s_x-s_y)/2 sin(2q) + t_xycos(2q)

s_1,2 = (s_x+s_y)/2 ± sqrt { [ (s_x-s_y)/2 ]² + t_xy² }
t_max = sqrt { [ (s_x-s_y)/2 ]² + t_xy² }
s_avg = (s_x+s_y)/2

 

key