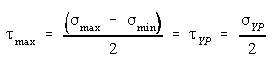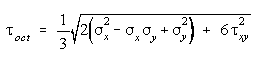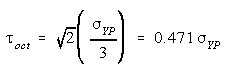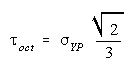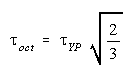Theories of Failure

Failure is generally perceived to be fracture or complete separation of a member. However, failure may also occur due to excessive deformation (elastic or inelastic) or a variety of other reasons.

During the latter part of the 19th century and continuing up to the present, a number of basic failure theories were proposed and tested on a few materials.¹  Most of the theories were based on the assumption that failure occurs when some physical variable such as stress, strain, or energy reaches a limiting value.

Deformation:

• Elastic deformation is temporary (reversible) and involves bond stretching.
• Plastic deformation is permanent (irreversible), and involves bond breaking.
• Fracture is catastrophic.

http://www.matse.psu.edu/matse81/Spring%202003/LectureNotes/

Classification System for Mechanical Failure Modes ⁴

 

Stress Theories

Maximum Principal Stress Theory (Rankine, Lamé)

Applied satisfactorily to many brittle materials, the theory is based on a limiting normal stress.  Failure occurs when the normal stress reaches a specified upper limit.¹

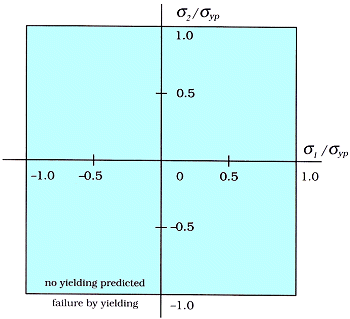
Failure is predicted when either of the principal stresses, σ1 or σ2, equals or exceeds the yield strength, σyp, of the material.3 σ1 < σyp σ2 < σyp

Examples Click on image for full size.

 

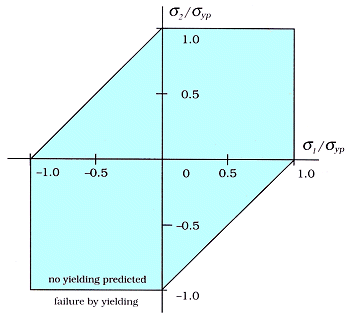
Maximum Shear Stress Theory (Tresca, Guest, Coulomb)

Applied satisfactorily to ductile materials, the theory is based on the concept of limiting shearing stress at which failure occurs.¹

Failure by yielding in a more complicated loading situation is assumed to occur when the maximum shearing stress in the material reaches a value equal to the maximum shearing stress in a tension test at yield.

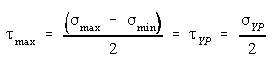
This yield criterion gives good agreement with experimental results for ductile materials; because of its simplicity, it is the most often used yield theory.²  The main objection to this theory is that it ignores the possible effect of the intermediate principal stress, σ₂.  However, only one other theory, the maximum distortional strain energy theory, predicts yielding better than does the Tresca theory, and the differences between the two theories are rarely more than 15%.

Failure is predicted when any of the three shear stresses corresponding to the principal stresses, σ1,2, equals or exceeds the shear stress corresponding to the yield strength, σyp, of the material in uniaxial tension or compression.3

Maximum Octahedral Shearing Stress Theory

Failure by yielding in a more complicated loading situation is assumed to occur when the octahedral shearing stress in the material reaches a value equal to the maximum octahedral shearing stress in a tension test at yield.

Plane stress case		Uniaxial stress case

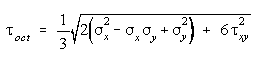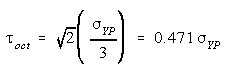Note: This theory gives the same results as the maximum distortion energy theory.

 

Strain Theories

Maximum Principal Strain Theory (Saint-Venant)

The theory is based on the assumption that inelastic behavior or failure is governed by a specified maximum normal strain.¹  Failure will occur at a particular part in a body subjected to an arbitrary state of strain when the normal strain reaches a limiting level.

Failure is predicted when either of the principal strains, resulting from the principal stresses, σ1,2, equals or exceeds the maximum strain corresponding to the yield strength, σyp, of the material in uniaxial tension or compression.3 σ1 - ν(σ2 + σ3) < σyp

 

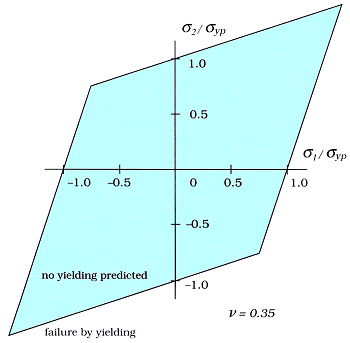
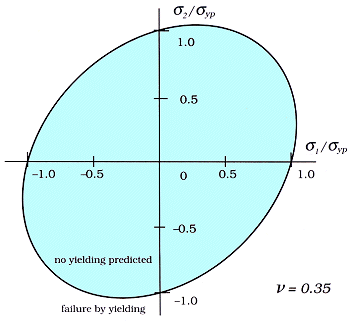
Total Strain Energy Theory (Beltrami-Haigh)

Applicable to many types of materials, the theory predicts failure or inelastic action at a point when the strain energy per unit volume exceeds a specified limit.¹

Failure is predicted when the total strain energy associated with the principal stresses, σ1,2, equals or exceeds the total strain energy corresponding to that for the yield strength, σyp, of the material in uniaxial tension or compression.3 σ12 + σ22 + σ32 -2ν(σ1σ2 + σ2σ3 + σ1σ3) < σyp2

 

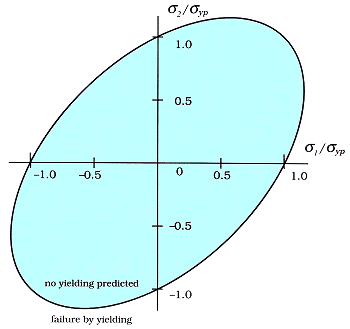
Maximum Distortion Energy Theory (Huber-Henky-von Mises)

The theory is based on a limiting energy of distortion, i.e. energy associated with shear strains.¹

Strain energy can be separated into energy associated with volume change and energy associated with distortion of the body. The maximum distortion energy failure theory assumes failure by yielding in a more complicated loading situation to occur when the distortion energy in the material reaches the same value as in a tension test at yield.

This theory provides the best agreement between experiment and theory and, along the Tresca theory, is very widely used today.²

Note: This theory gives the same results as the octahedral shear stress theory.

Failure is predicted when the distortional energy associated with the principal stresses, σ1,2, equals or exceeds the distortional energy corresponding to that for the yield strength, σyp, of the material in uniaxial tension or compression.3 0.5 ( (σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2) < σyp2

 

Summary

Of the failure criteria, the Tresca is the most conservative for all materials, the von Mises the most representative for ductile materials, and the Rankine the best fit for brittle materials.³

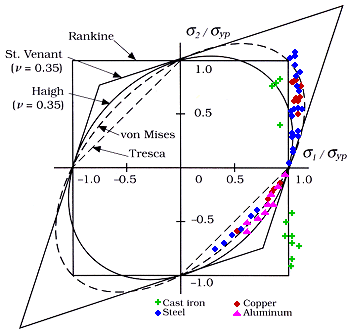
Laminated-Composite Failure Envelopes

More on failure theories

 

Below is a summary of two of most popular theories of failure applied to a simple uniaxial stress state and to a pure shear stress state.

Failure Criteria
Theory	Loading		Relationship
	Uniaxial	Pure Shear
Maximum principal stress	σmax = σYP	σmax = τYP	τYP = σYP
Maximum principal strain	εmax = σYP / E	εmax = 5τYP / 4E	τYP = 0.8 σYP
Maximum octahedral shear stress		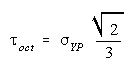	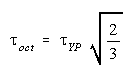τYP = 0.577 σYP
Maximum distortional energy density			τYP = 0.577 σYP
Maximum shear stress	τmax = σYP / 2	τmax = τYP	τYP = 0.5 σYP

 

References

1. Mechanics of Wood and Wood Composites, by J. Bodig & B.A. Jayne, Krieger Publishing, 1993, pp. 314-5.
2. The Science and Technology of Civil Engineering Materials, by J.F. Young, S. Mindess, R.J. Gray, & A. Bentur, Prentice Hall, 1998, pp. 115-7.
3. "Failure Prediction and Avoidance," Experimental Stress Analysis Notebook, Issue 22, Dec. 1993, Measurements Group, pp. 6-11.
4. Failure of Materials in Mechanical Design - Analysis Prediction Prevention, by J. A. Collins, John Wiley and Sons, 1981, pp. 6-8.