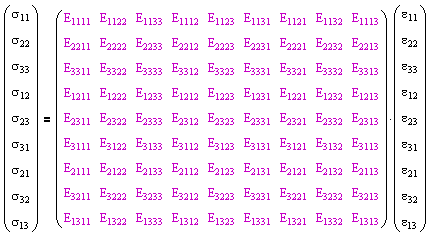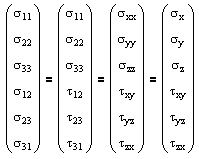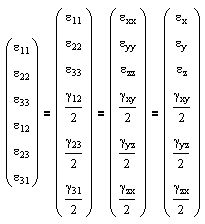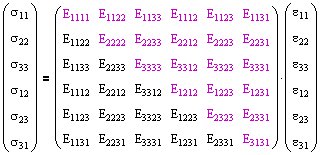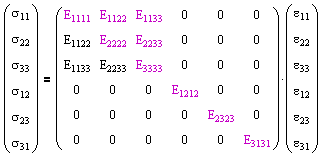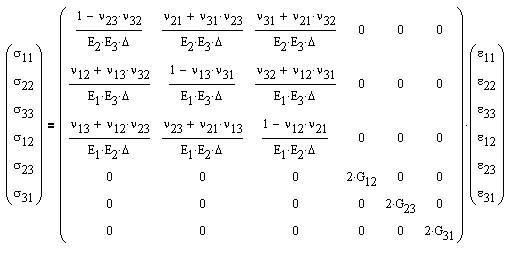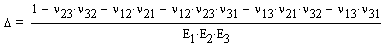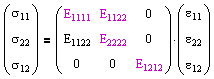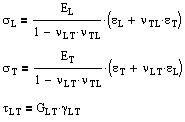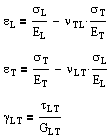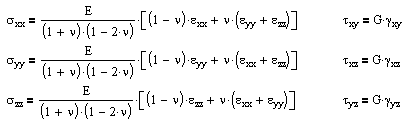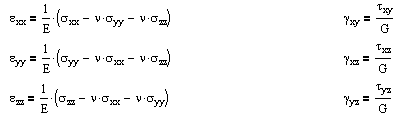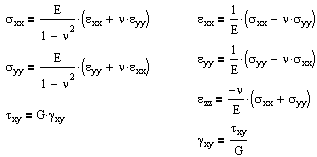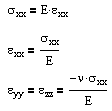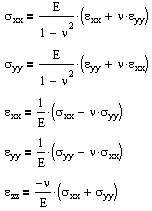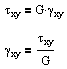|
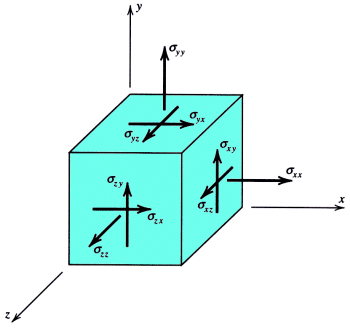
The concepts of stress and strain are introduced to provide scalability between geometries for laboratory specimens and real-world applications. The generalized Hooke's law for relating stress and strain is given by
where the 81 components of the fourth-order tensor Eijkl are known as the elastic constants. This equation can be represented in matrix form as follows. |
 |
For materials described by anisotropic, linear-elastic behavior, it can be shown from symmetry and thermodynamics that the elastic constants tensor can be reduced to 21 distinct components.
taken by Mike Crites, Jose Soto, & Jeff Thomas, October 1997
Or as a series of linear equations,
σxx = C11εxx + C12εyy + C13εzz + C14γxy + C15γxz + C16γyz
&sigmayy = C12εxx + C22εyy + C23εzz + C24γxy + C25γxz + C26γyz
σzz = C13εxx + C23εyy + C33εzz + C34γxy + C35γxz + C36γyz
σxy = C14εxx + C24εyy + C34εzz + C44γxy + C45γxz + C46γyz
σxz = C15εxx + C25εyy + C35εzz + C45γxy + C55γxz + C56γyz
σyz = C16εxx + C26εyy + C36εzz + C46γxy + C56γxz + C66γyz
For generally orthotropic, linear-elastic materials (wood, laminated plastics, cold rolled steels, reinforced concrete, various composite materials, and forgings), which posses a plane of elastic symmetry, the number of independent elastic constants reduces to nine.
Or in more conventional terms,
where
Or as a series of linear equations,
σxx = C11εxx + C12εyy + C13εzz
σyy = C12εxx + C22εyy + C23εzz
σzz = C13εxx + C23εyy + C33εzz
σxy = C44γxy
σxz = C55γxz
σyz = C66γyz
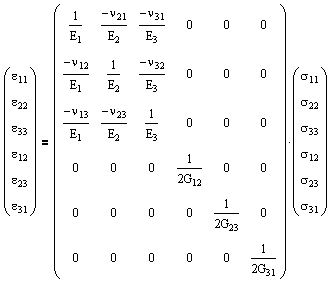
Alternatively we can rearrange in terms of strain.
|
For specially orthotropic, linear-elastic materials in two dimensions (longitudinal and transverse), the number of independent elastic constants reduces to four (EL, ET, νLT, νTL). Or as linear equations, where the constants are related by νLTET = νTLEL, Alternatively we can rearrange these stress formulas in terms of strain. |
For transversely isotropic, linear-elastic materials in three dimensions, where T' represents the axis perpendicular to the L and T axes, the following relationships hold for the five independent elastic constants (EL, ET, GLT, νLT, νTT').
ET = ET'
GLT = GLT'
νLT = νLT'
GTT' = ET / 2(1+νTT')
For isotropic, linear-elastic materials, this number is further reduced to two distinct components in both two and three dimensions. The three-dimensional equations are:
source
where the constants are related by G = E / 2(1+ν). E and ν can be determined from a uniaxial tension test, and G can be determined from a torsion test. And alternatively we can rearrange these stress formulas in terms of strain.
|
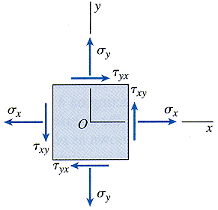
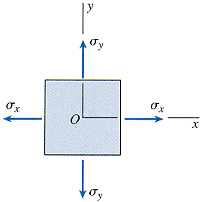
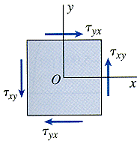
For two-dimensional or plane stresses (σzz = τxz = τyz = 0), the isotropic equations reduce to the following. Normal stresses are considered positive for tension and negative for compression. Shear stresses are considered positive when the directions associated with the subscripts are plus-plus or minus-minus (first or third quadrants) and negative when the directions are plus-minus or minus-plus (second or fourth quadrants). The following special cases of plane stress can also be studied.
|
For an isotropic material,
- E, G and K > 0
- -1 < ν < 0.5
For an orthotropic material,
- EL, ET, ET', GLT, GLT' and GTT' >0
- (1-νLT νTL), (1-νLT' νT'L) and (1-νTT' νT'T) > 0
- 1 - νLT νTL - νLT' νT'L - νTT' νT'T - 2νLT νTT'νT'L > 0