The elastic constants, E - modulus of elasticity and v - Poisson's ratio, were originally defined under a uniaxial stress state. We normally think of performing a uniaxial tensile test to determine these constants. Frequently, however, we find it inconvenient to perform uniaxial tensile tests for elastic constants. It may be time consuming, expensive or perhaps impractical to prepare tensile specimens from beams or other structural members.
Fortunately, we can use other tests to determine elastic constants. The only requirement is that the theoretical state of stress at the point of measurement be known (it need not be a uniaxial stress state). For accurate results this means that the theory should accurately predict the state of stress and that the strain gradient not be too great in the neighborhood of the measurements.
The flexure stress state in simple beams is accurately predicted by elementary theory. Additionally, at the top or bottom of such beams the stress state on the differential element is a uniaxial stress state. This makes a simple beam bending test an excellent test for elastic constants.
The flexural stresses (also called normal stresses due to bending or fiber stress) is given by the equation:
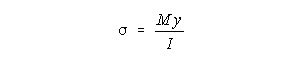
where M is the bending moment, y is distance from the neutral axis of bending (centroidal axis perpendicular to the loading direction) and I is the moment of inertia (second moment of area) with respect to the neutral axis.
At the top and bottom surfaces of the beam (Figure 1) the shearing stress is zero and the state of stress on the differential element is one of uniaxial compression or tension (Figure 2).
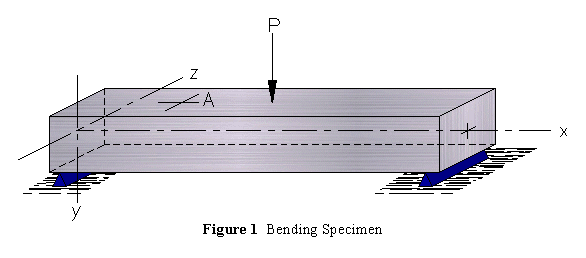
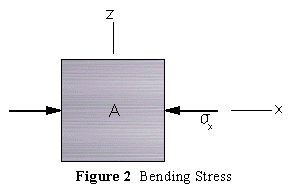
At other locations on the beam we also encounter transverse shear stress given by
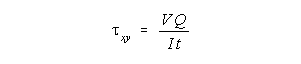
The flexure stress formula generally gives excellent results as long as we stay away from loading points and supports. Also, results will be better at the top and bottom extremities than elsewhere because of the presence of
stress in the beam. The
stress should be quite small as long as we stay a sufficient distance from load and support points. It is not predicted by elementary theory, but it is present and thus results in a biaxial state of normal stress at points other than top and bottom of the beam.
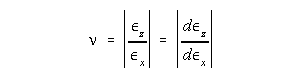
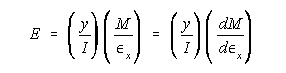
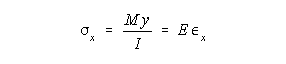
Saint-Venant (a French mathematician) discovered that the stress state predicted by elementary theory does not hold in regions near loads, supports or discontinuities. He observed that at sufficient distance from these localized distortions the stress state returns to that predicted by elementary theory (the implication is that the distance is not great). This principle is known as Saint-Venant's principle. As a rule of thumb it can be assumed that the state of normal stress is accurately given by the flexure stress formula provided we stay a distance greater than one or two times the depth of the beam away from load and support points.
- Simply support a beam which has a strain rosette on the top (or bottom) surface. Select load increments which will permit about 10 load readings without exceeding a maximum flexural stress of 20,000 psi (note that the maximum flexural stress will not be at your gage location).
- Sketch the loading configuration showing the beam dimensions, support and loading points and gage locations.
- Load the beam and record axial and
transverse strains (
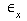and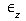 
as per figure above) for each load increment.
- Plot two graphs:
- load vs axial strain (
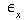) - transverse strain vs axial strain
-
Use absolute values of strain to keep the curves in the first quadrant
- load vs axial strain (
-
From the slopes of the curves, as determined by the method of least squares, determine the modulus of elasticity E and Poisson's ratio v using the relationships:
-
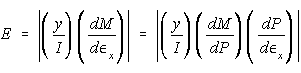
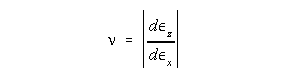
Note that
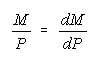is a function only of geometry.
Mechanics of Materials, by Higdon et al., 4th Ed., Wiley, 1985, Chapter 6, pp 237-256.
Mechanics of Materials, by Hibbeler, Macmillan, 1991, pp 247-257, 88, 99.
Mechanics of Materials, by Hibbeler, Macmillan, 2nd Ed, 1994, pp 286-295, 92, 105.