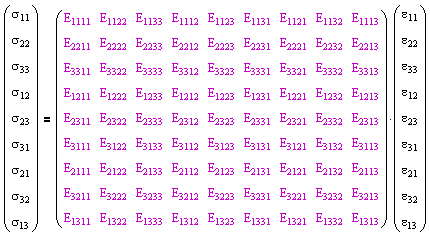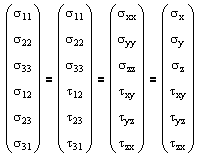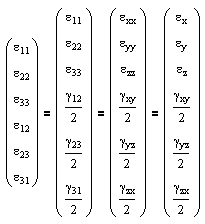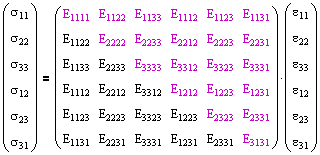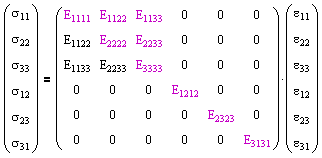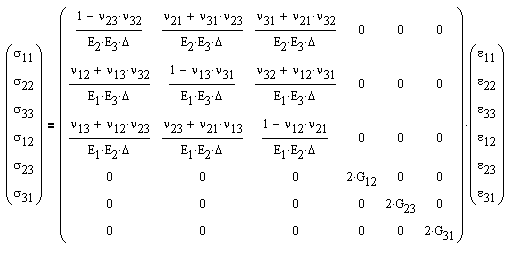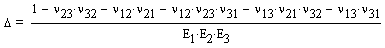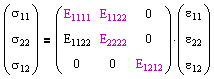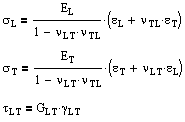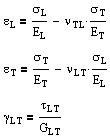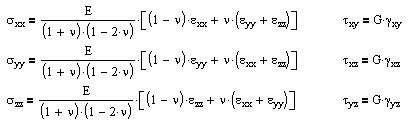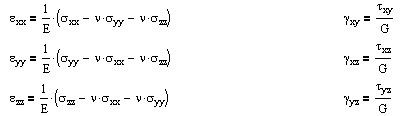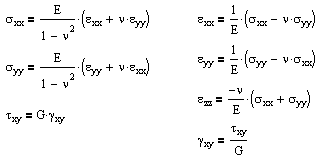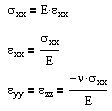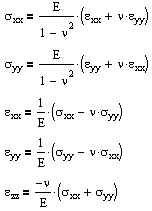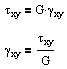Generalized Hooke's Law

The concepts of stress and strain are introduced to provide scalability between geometries for laboratory specimens and real-world applications. The generalized Hooke's law for relating stress and strain is given by  σij = Eijkl εkl where the 81 components of the fourth-order tensor Eijkl are known as the elastic constants.  This equation can be represented in matrix form as follows.

Note that symbols with mixed subscripts are often represented by τ and γ and the subscripts 1, 2 and 3 may be replaced by x, y, and z.  The first subscript identifies the face on which it acts, and the second subscript gives the direction on that face.

For materials described by anisotropic, linear-elastic behavior, it can be shown from symmetry and thermodynamics that the elastic constants tensor can be reduced to 21 distinct components.

		taken by Mike Crites, Jose Soto, & Jeff Thomas, October 1997

Or as a series of linear equations,

σ_xx = C₁₁ε_xx + C₁₂ε_yy + C₁₃ε_zz + C₁₄γ_xy + C₁₅γ_xz + C₁₆γ_yz
&sigma_yy = C₁₂ε_xx + C₂₂ε_yy + C₂₃ε_zz + C₂₄γ_xy + C₂₅γ_xz + C₂₆γ_yz
σ_zz = C₁₃ε_xx + C₂₃ε_yy + C₃₃ε_zz + C₃₄γ_xy + C₃₅γ_xz + C₃₆γ_yz
σ_xy = C₁₄ε_xx + C₂₄ε_yy + C₃₄ε_zz + C₄₄γ_xy + C₄₅γ_xz + C₄₆γ_yz
σ_xz = C₁₅ε_xx + C₂₅ε_yy + C₃₅ε_zz + C₄₅γ_xy + C₅₅γ_xz + C₅₆γ_yz
σ_yz = C₁₆ε_xx + C₂₆ε_yy + C₃₆ε_zz + C₄₆γ_xy + C₅₆γ_xz + C₆₆γ_yz

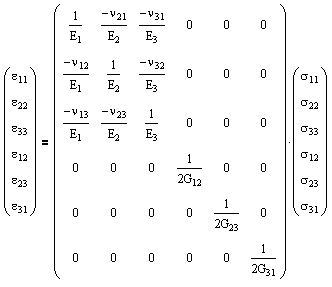
For generally orthotropic, linear-elastic materials (wood, laminated plastics, cold rolled steels, reinforced concrete, various composite materials, and forgings), which posses a plane of elastic symmetry, the number of independent elastic constants reduces to nine.

		Koch, P. 1972a. Utilization of the southern pines. I. The raw material. USDA Forest Service Agricultural Handbook No. 420. 733 pp. Koch, P. 1972b. Utilization of the southern pines. II. The raw material. USDA Forest Service Agricultural Handbook No. 420. 926 pp.

Or in more conventional terms,

where

Or as a series of linear equations,

σ_xx = C₁₁ε_xx + C₁₂ε_yy + C₁₃ε_zz
σ_yy = C₁₂ε_xx + C₂₂ε_yy + C₂₃ε_zz
σ_zz = C₁₃ε_xx + C₂₃ε_yy + C₃₃ε_zz
σ_xy = C₄₄γ_xy
σ_xz = C₅₅γ_xz
σ_yz = C₆₆γ_yz

Alternatively we can rearrange in terms of strain.

For specially orthotropic, linear-elastic materials in two dimensions (longitudinal and transverse), the number of independent elastic constants reduces to four (EL, ET, νLT, νTL). Or as linear equations, where the constants are related by νLTET = νTLEL, Alternatively we can rearrange these stress formulas in terms of strain.

For transversely isotropic, linear-elastic materials in three dimensions, where T' represents the axis perpendicular to the L and T axes, the following relationships hold for the five independent elastic constants (E_L, E_T, G_LT, ν_LT, ν_TT').

ET = ET' GLT = GLT' νLT = νLT' GTT' = ET / 2(1+νTT')

For isotropic, linear-elastic materials, this number is further reduced to two distinct components in both two and three dimensions.  The three-dimensional equations are:

		source

where the constants are related by G = E / 2(1+ν).  E and ν can be determined from a uniaxial tension test, and G can be determined from a torsion test.  And alternatively we can rearrange these stress formulas in terms of strain.

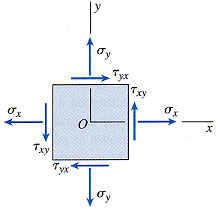
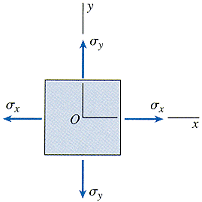
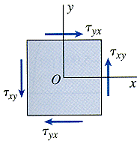
For two-dimensional or plane stresses (σzz = τxz = τyz = 0), the isotropic equations reduce to the following.  Normal stresses are considered positive for tension and negative for compression.  Shear stresses are considered positive when the directions associated with the subscripts are plus-plus or minus-minus (first or third quadrants) and negative when the directions are plus-minus or minus-plus (second or fourth quadrants). The following special cases of plane stress can also be studied. Uniaxial stress (σyy = τxy = 0) Biaxial stress (τxy = 0) Pure shear (σxx = σyy = 0)

For an isotropic material,

• E, G and K > 0
• -1 < ν < 0.5

For an orthotropic material,

• E_L, E_T, E_T', G_LT, G_LT' and G_TT' >0
• (1-ν_LT ν_TL), (1-ν_LT' ν_T'L) and (1-ν_TT' ν_T'T) > 0
• 1 - ν_LT ν_TL - ν_LT' ν_T'L - ν_TT' ν_T'T - 2ν_LT ν_TT'ν_T'L > 0