We begin by addressing an earlier omission. We have discussed that we
did not define any type of multiplication between vectors. While there
is no operation that will have all of the properties that we believe
multiplication should have, the inner product or dot product
comes close. For vectors
![]() and
and
![]() in
in
![]() , we define the
standard inner product as
, we define the
standard inner product as
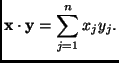 |
(1) |
| (2) |
Note that this form of multiplication takes two vectors and produces a
real number. Your initial thoughts on vector multiplication probably
expected a vector as the result. This would be problematic. In fact, the
cross product on
![]() is about as close as we get. This aside, the
inner product has several properties we associate with multiplication
is about as close as we get. This aside, the
inner product has several properties we associate with multiplication
![% latex2html id marker 1028
\framebox[5.0in]{ \parbox{4.0in}{\begin{theorem_type...
...,$\mathbf{y}$, and $\mathbf{z}$\ and real numbers $\alpha$. \end{theorem_type}}}](img7.png)
In fact, any operation which takes two vectors into a real number and has these properties is considered an inner product.
We should also note that the inner product between two vectors can be zero.
If this occurs, we say that the vectors are orthogonal
or perpendicular. This terminology comes from the relationship in
![]()
| (3) |