


Next: Proving a Function is
Up: Measuring the Size of
Previous: Inner Product
The inner products relays two types of information about vectors: their length
or magnitude, and their relative orientation. While this may be difficult to
visualize in
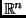 , you won't be betrayed by visualizing
, you won't be betrayed by visualizing
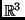 . We
solidify the notion of length in this manner. We define the Euclidean norm of
a vector
. We
solidify the notion of length in this manner. We define the Euclidean norm of
a vector
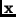 in
in
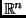 as
as
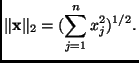 |
(4) |
By using this definition with that of the inner product we see that
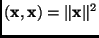 |
(5) |
The norm (and therefore the inner product) measures the length, size, magnitude,
or strength of the vector depending on what interpretation you are giving the
vector.
There is nothing special about the Euclidean norm. It is properties make it special. We recognize them as
As with the inner product, any function which takes a vector into a real number
and satisfies these properties is called a norm. Item number (4) is
refereed to as the triangle inequality.
We have already seen that inner products and norms are related. Another
such relation is in the form of the Cauchy-Schwarz Inequality which
says that for any two vectors
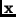 and
and
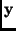
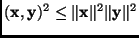 |
(6) |
Showing that a function you believe to measure size is indeed a norm can be a tricky proposition. In fact, showing the Euclidean norm is a actually a norm requires the use of the Cauchy-Schwarz Inequality to prove the
Triangle Inequality.
If you have never seen norm proved to be so, it is worth a quick peek.



Next: Proving a Function is
Up: Measuring the Size of
Previous: Inner Product
Michael HIlgers
2002-10-07
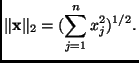
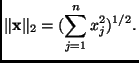
![% latex2html id marker 1056
\framebox[5.0in]{ \parbox{4.0in}{\begin{theorem_type...
... $\mathbf{x}$\ and $\mathbf{y}$\ and real numbers $\alpha$. \end{theorem_type}}}](img14.png)
![]() and
and
![]()