Proof.
Let
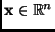
. We prove the proprieties in order.
- Since
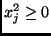 for
for
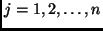 . Then
The positive branch of the square root function is an increasing function so we have
. Then
The positive branch of the square root function is an increasing function so we have
- Note that
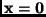 is equivalent to
is equivalent to 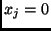 for
for
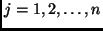 . Of course, this quickly implies
There is a subtle point here. We also need to show
implies that
. Of course, this quickly implies
There is a subtle point here. We also need to show
implies that 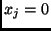 for
for
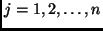 . There are many reasonable candidates for norms that fail this property. It is often easier to prove the
contrapositive. Recall the contrapositive of (
. There are many reasonable candidates for norms that fail this property. It is often easier to prove the
contrapositive. Recall the contrapositive of (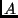 implies
implies 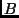 ) is (
) is (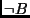 implies
implies 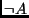 ). These expressions are logically equivalent. Prove one and you have proved the other. So we assume
). These expressions are logically equivalent. Prove one and you have proved the other. So we assume
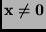 . This means there is an index
. This means there is an index 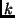 such that
such that
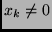 . Since
. Since
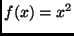 has only one root at
has only one root at 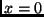 , then we know
, then we know
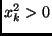 . Furthermore
. Furthermore
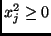 for the remaining components of
for the remaining components of
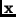 . Hence,
Using the increasing property of the square root function, we get
. Hence,
Using the increasing property of the square root function, we get
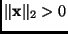 . (This may seems like too many words to show something that is obvious, but this obvious property fails enough mathematicians had to create the concept of semi-norm).
. (This may seems like too many words to show something that is obvious, but this obvious property fails enough mathematicians had to create the concept of semi-norm).
- Using the fact that
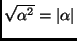 , quickly get this property.
, quickly get this property.
- The triangle inequality is also the problematic part of showing a function is a norm. Let
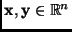 . Then
. Then

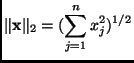
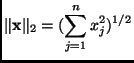
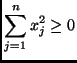
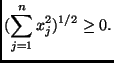
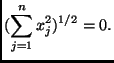
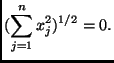
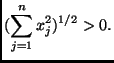
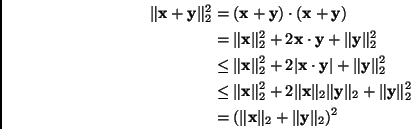
![]()