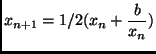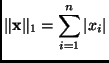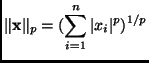Next: Matrix Norms
Up: Measuring the Size of
Previous: Proving a Function is
Using the standard Euclidean norm in the course of a vector-based numerical algorithm is not computationally wise. The square root function is the problem point. Suppose you wish to calculate the 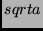 . The following steps are involved.
. The following steps are involved.
- The number
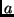 is rescaled to a number
is rescaled to a number 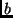 such that
such that
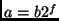 with
with
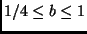 and
and 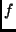 an even integer. Many numerical methods use a scaling process to keep from working with numbers that are too large or too small.
an even integer. Many numerical methods use a scaling process to keep from working with numbers that are too large or too small.
- Linear interpolation is used to produce an initial guess
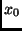 .
.
- The iteration process is based Newton's method and is easily seen to be
- A certain number of iterations is used to produce an estimate of
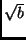 . Since
. Since 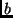 was chosen to fit in a certain range, the number of iterations is know a priori.
was chosen to fit in a certain range, the number of iterations is know a priori.
-
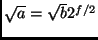 .
.
These process can get expensive, particularly if it is enclosed in one or several loops in an iterative process.
So numerical modelers often appeal to vector norms other than the Euclidean norm. Once popular choice is the so-called maximum norm
It measures the size of a vector in terms of its largest component.
Another common choice is the
This avoids the root finding problem of the Euclidean norm.
Of course, these are not the only choice. There is the general family
where we have consider the cases where 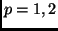 . In general, these have the root finding problem attached to them except when
. In general, these have the root finding problem attached to them except when 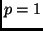 .
.



Next: Matrix Norms
Up: Measuring the Size of
Previous: Proving a Function is
Michael HIlgers
2002-10-07
![]() . The following steps are involved.
. The following steps are involved.