Normal Stresses in Beams

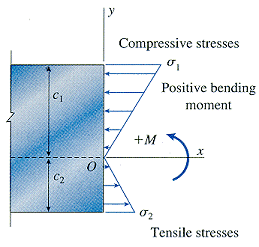
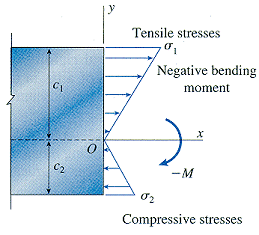
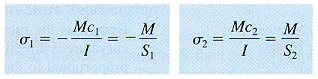Transverse strains (normal strains in the y and z directions) are present in a beam due to Poisson's ratio, but there are no transverse stresses because the beam is free to deform in those directions. (i.e. longitudinal elements in a beam in pure bending are in a state of uniaxial stress -- tension or compression)  These stresses act over the entire cross section and vary in intensity depending on the shape of the stress-strain diagram and the dimensions of the cross section.  For a linear elastic material,

 

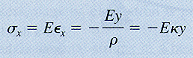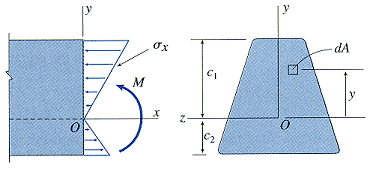location of neutral axis

The neutral axis passes through the centroid of the cross-sectional area when the material follows Hooke's law and there is no axial force acting on the cross section.

see A1

 

moment-curvature relationship

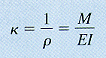
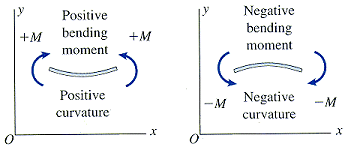
where I is the moment of inertia (units: in4, m4) of the cross-sectional area with respect to the neutral axis.  Note the following sign convention.

see A5

table

W-shape beams by Dr. Chien-Chung Chen

efficient beam design

special problem

 

flexure formula

Stresses calculated from the flexure formula are called bending stresses or flexural stresses.

 

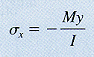
see M8.4

 

maximum stresses at a cross-section

The maximum tensile and compressive bending stresses occur at points (c1 and c2) furthest from the neutral surface.

where S1 and S2 are called section moduli (units: in3, m3) of the cross-sectional area.  Section moduli are commonly listed in design handbooks.

 

limitations

The above equations only work when we bend around a principal (symmetric) axis.  These equations were derived for pure bending of prismatic beams composed of homogeneous, linearly elastic materials.  Nonuniform bending will cause warping (cross sections will not remain plane).  However, we can use pure bending equations to approximate nonuniform bending stresses.  The above equations are not valid near stress concentrations (i.e., near changes in shape and loading discontinuities).