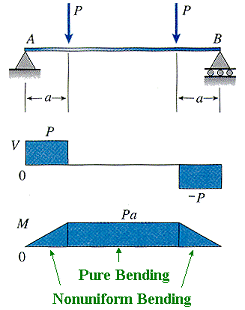
Most beams experience both bending moments and shear forces (nonuniform bending), which produce both normal and shear stresses.
- The normal stresses are calculated with the flexure formula.
- The shear stresses will be discussed below.
 |
 |
assumptions
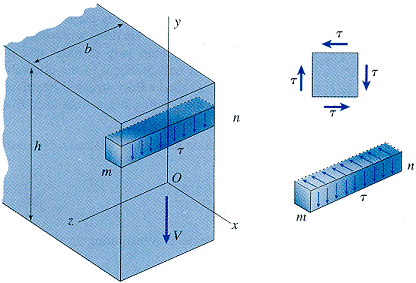
- prismatic beam of linear elastic material with small beam deflections
- shear stresses acting on the cross section are parallel to the shear force
- shear stresses are uniformly distributed across the width of the beam (but can vary over the height)
57% e-glass fibers in a polyester matrix
shear stress formula
where
- τ = shear stress at desired point in the cross section
- V = shear force at that cross section
- Q = first moment of the cross-sectional area above the level at which the shear stress τ is being evaluated (Q varies with y, therefore τ varies with y)
see M9.3
- I = moment of inertia for entire cross section
- b = width of cross section where shear stress τ is being evaluated
shear stresses in rectangular beams
approximations for circular beams
approximations for flanged beams
shear concepts in percussion instruments
limitations
- Accuracy of the shear stress formula depends on the height-to-width ratio of the cross section -- it is more accurate for narrow beams. (h>>b)
- It is only valid for certain cross sections. (not for triangular or semicircular)