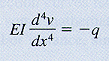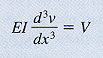Deflections by Integration of the Bending-Moment Equation

solution technique divide beam into regions of continuous M equations integrate each region twice to determine beam deflections v solve for two integration constants per region using: boundary conditions - deflections and slopes at the beam supports continuity conditions - deflections and slopes where regions meet symmetry conditions
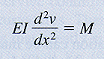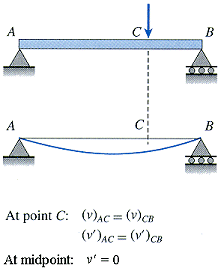
Symmetry conditions are not needed to solve for the integration constants. They are not independent of the boundary and continuity conditions but can be used in the place of these conditions.

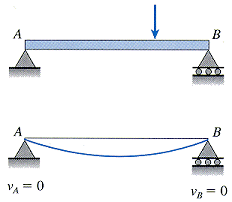
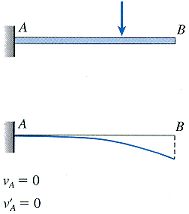
Boundary condition examples				Continuity and symmetry example

support examples

bio-joints

 

Deflections by Integration of the Shear-Force and Load Equations

solution technique divide beam into regions of continuous q equations integrate each region four times to determine beam deflections v solve for four integration constants per region using: boundary conditions - deflections and slopes at the beam supports continuity conditions - deflections and slopes where regions meet symmetry conditions shear force conditions bending moment conditions